报告人:曹喜望 、罗高骏
报告地点:淦昌苑D座320
报告时间:2024-04-20 9:30-11:30
报告一:A Tight Upper Bound on the Number of Nonzero Weights of a Constacyclic Codes
报告人:曹喜望
报告摘要:
For a simple-root  -constacyclic code
-constacyclic code 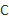 over
over 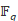 , let
, let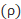 (resp.
(resp. 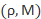 )be thesubgroup of the automorphism group of C generated by the cyclic shift
)be thesubgroup of the automorphism group of C generated by the cyclic shift 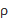 (resp.the subgroupgenerated by the cyclic shift
(resp.the subgroupgenerated by the cyclic shift 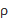 and the scalar multiplication group
and the scalar multiplication group 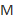 ). Let
). Let  be thenumber of orbits of a subgroup
be thenumber of orbits of a subgroup  of the automorphism group of
of the automorphism group of 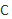 acting on
acting on 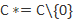 . In this talk, we show explicit formulas for
. In this talk, we show explicit formulas for  and
and 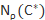 . Consequently,we derive a upperbound on the number of non-zero weights of
. Consequently,we derive a upperbound on the number of non-zero weights of 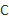 . We present some irreducible and reducible
. We present some irreducible and reducible  -constacyclic codes,which show that the upper bound is tight. A sufficient condition to guarantee
-constacyclic codes,which show that the upper bound is tight. A sufficient condition to guarantee 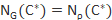 is provided. This is a joint work with Hanglong Zhang.
is provided. This is a joint work with Hanglong Zhang.
报告人简介:
曹喜望。南京航空航天大学理学院教授,博士生导师。北京大学获得博士学位。研究方向是有限域及其应用,在差集、指数和、有限域上的多项式、量子信息处理以及代数编码方面做出了出色的工作,其研究成果发表在相关领域的期刊IEEE Transaction on Information Theory、Finite Fields and their Applications、Design Codes and Cryptography、Science China(Mathematics)等,发表学术论文近200篇,其中SCI检索论文176篇。曹喜望教授先后多次访问过Sydney大学、南洋理工大学,香港科技大学、台湾中央研究院、北京国际数学中心、南开大学陈省身数学研究所等。2010年入选江苏省“青蓝工程”学术带头。主持完成国家自然科学基金项目5项和省部级科研项目多项。2017年获得江苏省科学技术奖。
报告二:On the Weights of Linear Codes with Prescribed Automorphisms
报告人:罗高骏
报告摘要:
The number of nonzero weights of a linear code is essential in coding theory as it unveils salient properties of the code, such as its covering radius. In this paper, we establish two upper bounds on the number of nonzero weights of a linear code with prescribed automorphism. Our bounds are applicable for almost all linear codes and tighter than previously known bounds. Examples confirm that our bounds are sharp on numerous occasions. In addition, we give an infinite family of linear codes that attain our bounds with equality.
报告人简介:
罗高骏,南京航空航天大学,副研究员。2019年博士毕业于南京航空航天大学,导师曹喜望教授。2021年至2024年于新加坡南洋理工大学从事博士后研究工作,合作导师Ling San教授。主要研究方向为代数编码理论、序列设计与量子信息。近五年,以第一/通讯作者发表SCI检索论文20余篇,包括IEEE Trans系列10篇。曾获得江苏省科学技术奖。2022年至今,担任期刊COAM(《Computational and Applied Mathematics》)的 Associate Editor。曾应邀访问土耳其Sabanci大学,韩国庆北国立大学。
邀请人:方伟军
审核人:魏普文